Il moto circolare uniforme è il movimento compiuto da un corpo (punto materiale) che si muove su un piano su una traiettoria circolare a velocità (angolare) costante. In questo tipo di moto piano, il punto materiale percorre archi di circonferenza uguali in intervalli di tempo uguali (ovvero, il vettore posizione che congiunge il punto P al centro della traiettoria circolare spazza angoli uguali in tempi uguali).
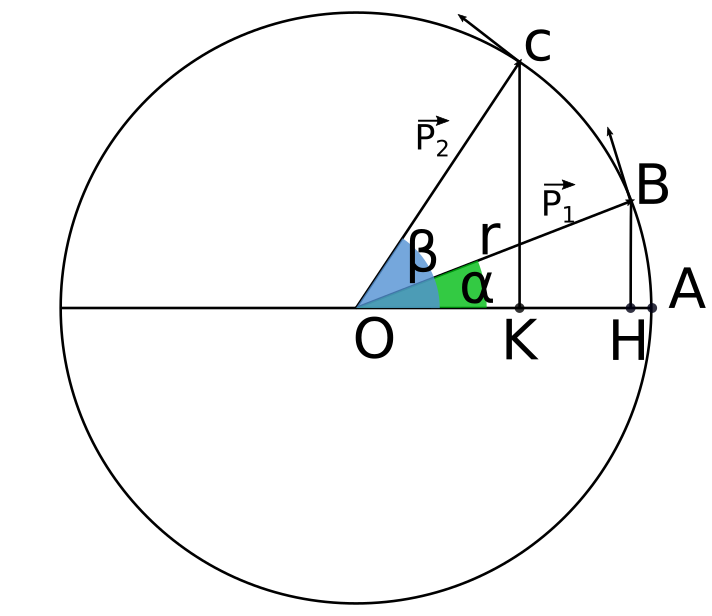
Il punto P si muove lungo la traiettoria circolare con una velocità costante percorrendo archi di circonferenza uguali in intervalli di tempo uguale per cui il vettore posizione spazza angoli uguali in tempi uguali. Un giro completo descrive un angolo di 2π in un tempo T (detto periodo) per cui la sua velocità angolare, detta pulsazione, è ω=2π/T.
Pertanto, essendo costante la distanza dal centro (pari alla misura del raggio r), il movimento può essere descritto con una legge oraria in cui si legano angolo e tempo:
θ(t)=θ0+ωt (leggi: teta di t uguale a teta zero più omega t)
dove
- la lettera greca θ (teta) rappresenta l'angolo formato dal vettore posizione (congiungente il centro O con il punto P) e un diametro preso come riferimento;
- l'angolo θ0 rappresenta l'angolo iniziale (solitamente posto uguale a zero);
- ω è la velocità angolare, t il tempo (rispetto ad un istante iniziale posto uguale a zero).
