- Dettagli
- Categoria: Fisica
- Visite: 471
|
Lettera Greca
|
Minuscolo
|
Unicode
|
Maiuscolo
|
Unicode
|
|
alfa
|
α
|
03b1
|
A
|
0391
|
|
beta
|
β
|
03b2
|
B
|
0392
|
|
gamma
|
γ
|
03b3
|
Γ
|
0393
|
|
delta
|
δ
|
03b4
|
Δ
|
0394
|
|
epsilon
|
ϵ
|
03b5
|
E
|
0395
|
|
zeta
|
ζ
|
03b6
|
Z
|
0396
|
|
eta
|
η
|
03b7
|
H
|
0397
|
|
teta
|
θ
|
03b8
|
Θ
|
0398
|
|
iota
|
ι
|
03b9
|
I
|
0399
|
|
kappa
|
κ
|
03ba
|
K
|
039a
|
|
lambda
|
λ
|
03bb
|
Λ
|
039b
|
|
mu
|
μ
|
03bc
|
M
|
039c
|
|
nu
|
ν
|
03bd
|
N
|
039d
|
|
xi
|
ξ
|
03be
|
Ξ
|
039e
|
|
omicron
|
o
|
03bf
|
O
|
039f
|
|
pi
|
π
|
03c0
|
Π
|
03a0
|
|
ro
|
ρ
|
03c1
|
P
|
03a1
|
|
sigma
|
σ
|
03c3
|
Σ
|
03a3
|
|
tau
|
τ
|
03c4
|
T
|
03a4
|
|
ypsilon
|
υ
|
03c5
|
ϒ
|
03a5
|
|
fi
|
ϕ
|
03c6
|
Φ
|
03a6
|
|
chi
|
χ
|
03c7
|
X
|
03a7
|
|
psi
|
ψ
|
03c8
|
Ψ
|
03a8
|
|
omega
|
ω
|
03c9
|
Ω
|
03a9
|
Per inserire in un disegno Inkscape una lettera greca, selezionare il modo testo cliccando sullo strumento corrispondente e cliccare quindi CTRL + U digitando poi le 4 cifre esadecimali corrispondenti.
- Dettagli
- Categoria: Fisica
- Visite: 1182
Il moto circolare uniforme è il movimento compiuto da un corpo (punto materiale) che si muove su un piano su una traiettoria circolare a velocità (angolare) costante. In questo tipo di moto piano, il punto materiale percorre archi di circonferenza uguali in intervalli di tempo uguali (ovvero, il vettore posizione che congiunge il punto P al centro della traiettoria circolare spazza angoli uguali in tempi uguali).
Il punto P si muove lungo la traiettoria circolare con una velocità costante percorrendo archi di circonferenza uguali in intervalli di tempo uguale per cui il vettore posizione spazza angoli uguali in tempi uguali. Un giro completo descrive un angolo di 2π in un tempo T (detto periodo) per cui la sua velocità angolare, detta pulsazione, è ω=2π/T.
Pertanto, essendo costante la distanza dal centro (pari alla misura del raggio r), il movimento può essere descritto con una legge oraria in cui si legano angolo e tempo:
θ(t)=θ0+ωt (leggi: teta di t uguale a teta zero più omega t)
dove
- la lettera greca θ (teta) rappresenta l'angolo formato dal vettore posizione (congiungente il centro O con il punto P) e un diametro preso come riferimento;
- l'angolo θ0 rappresenta l'angolo iniziale (solitamente posto uguale a zero);
- ω è la velocità angolare, t il tempo (rispetto ad un istante iniziale posto uguale a zero).
- Dettagli
- Categoria: Fisica
- Visite: 1194
Il moto armonico è il moto rettilineo di un punto materiale con legge oraria: x(t)=r•cos(ωt), dove:
- x è l'ascissa - posizione sulla retta,
- t il tempo (misurato rispetto ad un istante preso come zero),
- r è l'ampiezza del moto (che oscilla fra - r e + r),
- cos è la funzione coseno (di un angolo),
- ωt è l'angolo argomento della funzione coseno dove:
- ω detta pulsazione è la velocità angolare
- t è il tempo (come sopra)
Tale tipo di moto corrisponde a quello compiuto dalla proiezione su un diametro della circonferenza di un punto materiale che si muove con moto circolare uniforme.

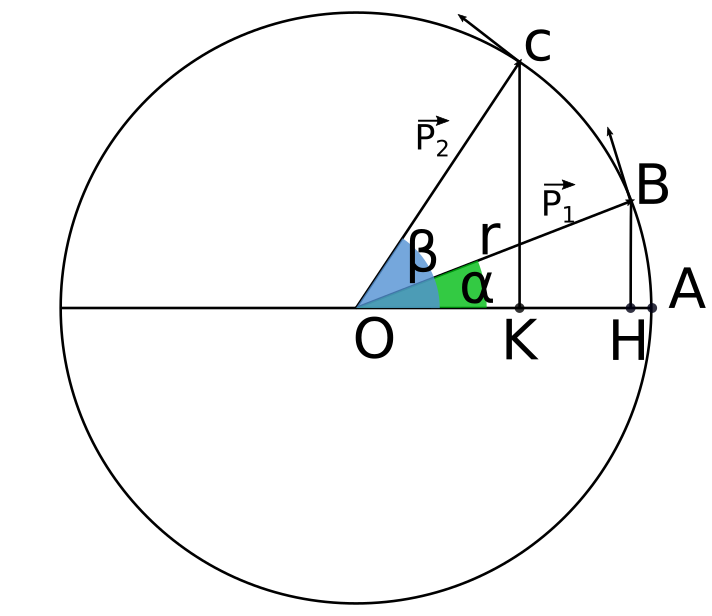
Per quest'ultimo tipo di movimento (moto piano su traiettoria circolare a velocità costante), la legge oraria è β(t)=β0+ωt (leggi: beta di t uguale a beta zero più omega t) dove:
- β è l'angolo formato dal vettore posizione OP (la cui misura è il raggio della circonferenza r),
- ω la velocità angolare,
- t il tempo trascorso
- β0 l'angolo all'istante 0;
Ricordando che:
- la proiezione H del punto P sul diametro di riferimento si ottiene tracciando una linea perpendicolare dal punto P alla retta che contiene il diametro di riferimento,
- gli angoli β descritti dal punto materiale P e,quindi, gli archi di circonferenza percorsi, sono positivi se la rotazione è antioraria;
risulta essere: OH=OP•cos(β), dove:
- OP è il vettore posizione del punto P che si muove di moto circolare uniforme;
- OH è il vettore posizione del punto H proiezione di P sul diametro di riferimento;
- β è l'angolo che varia con legge oraria β(t)=β0+ωt
Posto x(t)=OH, la posizione nel tempo del punto H (cioè la legge oraria), si può scrivere:
x(t)=r•cos(ωt)

